Hessian Matrix

Wikipedia Definition — In mathematics, the Hessian matrix or Hessian is a square matrix of second-order partial derivatives of a scalar-valued function, or scalar field. It describes the local curvature of a function of many variables.

Hessian matrices belong to a class of mathematical structures that involve second order derivatives. They are often used in machine learning and data science algorithms for optimizing a function of interest.

In Simple words — The Hessian matrix is a mathematical tool used to calculate the curvature of a function at a certain point in space.

The Hessian matrix plays an important role in many machine learning algorithms, which involve optimizing a given function. The Hessian is nothing more than the gradient of the gradient, a matrix of second partial derivatives.

The Hessian matrix was developed in the 19th century by the German mathematician Ludwig Otto Hesse and later named after him. Hesse originally used the term “functional determinants”.

Ludwig Otto Hesse

Several Applications

1. Second-derivative Test: For Convex function, the eigen-values of the Hessian matrix defines it local/global optima.
2. In Optimization: Used in large-scale Optimization.
3. To find out the Inflection Point.
4. To find out the Critical Point based on the nature of gradient.

Second-Order Derivative

We have already covered basic knowledge about First order and Second Order.

The second order derivatives are used to get an idea of the shape of the graph for the given function. Whether it will be upwards to downwards. It is based on concavity. The concavity of the given graph function is classified into two types: — Concave up and Concave down.

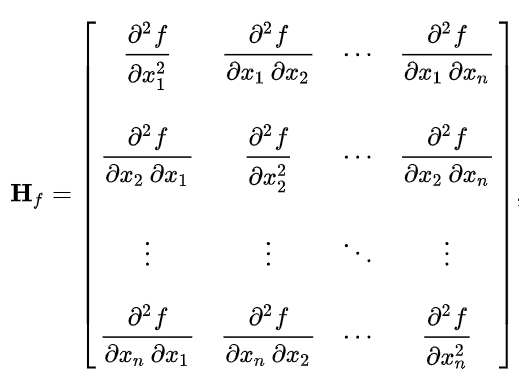
Suppose : — f: R^n → R

Formula for the Hessian matrix

for f(x,y)

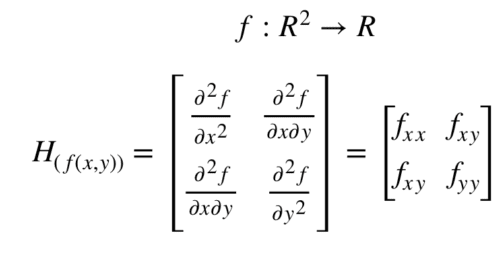
The determinant of the Hessian is also called the discriminant of f. For a two variable function f(x, y).

Discriminant of f(x, y)

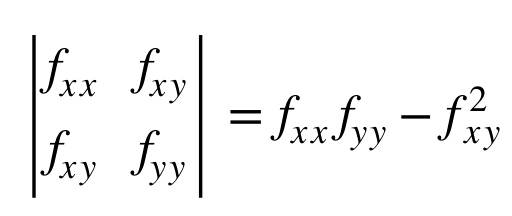
The Hessian matrix will always be a square matrix whose dimension will be equal to the number of variables of the function. For example, if the function has 3 variables, the Hessian matrix will be a 3×3 dimension matrix.

Furthermore, the Schwarz’s theorem (or Clairaut’s theorem) states that the order of differentiation does not matter, that is, first partially differentiate with respect to the variable x_1 and then with respect to the variable x_2 is the same as first partially differentiating with respect to x_2 and then with respect to x_1.

In Simple words, the Hessian matrix is a symmetric matrix.

Another wonderful article on Hessian. Example is taken from Algebra Practice Problems site.

let’s see an example to fully understand the concept:

Calculate the Hessian matrix at the point (1,0) of the following multivariable function:

We already know that second derivative of a function determines the local maximum (maxima) or minimum (minima), inflexion point values. These can be identified with the help of below conditions:

1. If the Hessian matrix is positive (Positive eigenvalues of Hessian matrix), the critical point is a local minimum of the function.

2. If the Hessian matrix is negative (Negative eigenvalues of Hessian matrix), the critical point is a local maximum of the function.

3. If the Hessian matrix is indefinite (when it is not possible to conclude positive and negative eigenvalues of Hessian matrix), the critical point is an inflexion point.

Thank you for reading. Links to other blogs: —

First order and Second order — Calculus
Statistical Inference 2 — Hypothesis Testing
Statistical Inference
Central Limit Theorem — Statistics
General Linear Model — 2
General and Generalized Linear Models
10 alternatives for Cloud based Jupyter notebook!!